線形走査法(linear probing)を使用するハッシュテーブルにおいて、最適なガベージコレクション戦略について考察する。
背景#
ハッシュテーブル(hash table)は、キーのハッシュ値を利用して値の挿入や検索を高速に行うデータ構造である。ハッシュテーブルでは、ハッシュ値が衝突した場合の処理方法として、連鎖法と開番地法の2種類の方法が存在する。
本ページでは、開番地法の一つである 線形走査法(linear probing) について考える。線形走査法は1954年に開発された方法で、ハッシュ値が衝突した場合、空きエントリが見つかるまで次の要素を探索する。線形走査法は非常にシンプルな実装方法であり、ハッシュ使用率が低い場合にはとても高速に動作する。そのため、簡易的なハッシュテーブル実装としてしばしば使われる1。
以下では、ハッシュテーブルの配列サイズを $N$ とする。
ハッシュテーブルでは、ハッシュ使用率が高くなるほど要素の挿入や検索に時間がかかることが知られている。キーのハッシュ値が一様乱数に従うとき、線形探査法のハッシュテーブルにおいて、 $k$ 個目の要素を挿入する際に必要なハッシュ値同士の比較回数の期待値 $M(N, k)$ は、以下のように近似できる2。
\begin{align} M(N, k) \simeq \frac{1}{2}\left( 1 + \frac{1}{(1-\rho)^2} \right) \end{align}
ただし、ここで $\rho := (k - 1)/N$ は挿入直前のハッシュ使用率である。また、検索に必要な比較回数の期待値も上記と同様に $M(N, k)$ となることが知られている。
式 $(1)$ が示す通り、線形探査法ではハッシュ使用率 $\rho$ の増加に伴い、挿入や探索に必要な計算量が増加する。そのため、線形探査法を高速に動作させるためには、ハッシュ使用率を低く保つための仕組みを導入する必要がある。
ハッシュ使用率を下げる方法として、ガベージコレクション(GC)と呼ばれる方法が知られている。これは、ハッシュ使用率がしきい値 $\rho_2$ を超えた場合に、エントリ削除を行うことでハッシュ使用率を $\rho_1$ ($0\leq \rho_1 < \rho_2<1$)まで下げる方法である。
ガベージコレクションにおいて、パラメータ $\rho_1$ は実行速度とメモリ効率の両方に影響を与える重要な要素である。 $\rho_1$ の値が大きいほど、ハッシュテーブルへの挿入や検索に必要な計算量が増加してしまう。一方、$\rho_1$ の値が小さいほどガベージコレクションで削除するエントリの数が増え、メモリの使用効率が悪くなる。以上のように、$\rho_1$ の値は、時間と空間のトレードオフを考慮しながら適切に決める必要がある。
最適なGC戦略#
さて、ガベージコレクション後のハッシュ使用率 $\rho_1$ が与えられた場合、挿入や検索の計算量を最小化するためには、どのような $\rho_2$ の値を設定すればよいだろうか。 $\rho_2$ の値が小さすぎると、頻繁にガベージコレクションを実行する必要が生じる。逆に、$\rho_2$ の値が大きすぎると、線形走査法の計算量が増え、エントリの挿入や検索に時間がかかってしまう。つまり、$\rho_2$ の値は大きすぎても小さすぎても望ましくなく、区間 $(\rho_1, 1)$ の間に最適な値が存在すると考えられる。
以下のような状況設定において、 $\rho_2$ の最適値を求めたい。
- エントリの挿入や検索に使用するキーは、一様乱数に従う
- エントリの挿入 $1$ 回に対して、検索が $a-1$ 回発生する
- 1回のGCにおけるハッシュ値の比較回数は $2N$ 回である
- 挿入1回あたりに平均化したハッシュ値の比較回数の期待値を最小化ように $\rho_2$ を決める
式で表すと、
\begin{align} \min_{\rho_2} \frac{1}{N(\rho_2 - \rho_1)} \left( 2N + \frac{a}{2} \sum_{k=\lfloor N \rho_1 \rfloor}^{\lfloor N \rho_2 \rfloor} \left( 1 + \frac{1}{(1 - \rho)^2} \right) \right) \end{align}
となる。この最小化問題に対し、和を積分で置き換えて近似し、式を整理すると最小化問題
\begin{align} \min_{\rho_2} \frac{1}{\rho_2 - \rho_1} \left( 2 + \frac{a}{2} \left( \rho_2 - \rho_1 + \frac{1}{1 - \rho_2} - \frac{1}{1 - \rho_1} \right) \right) \end{align}
が得られる。
式 (3) の近似した最小化問題に対し、いくつかの $\rho_1, a$ を与えて最適解を求めた。最適解の求解には Wolfram Alpha を使用した。各 $\rho_1, a$ に対する最適値とその時の目的関数値を以下に示す。
表1: $\rho_2$の最適値
| $\rho_1=0.1$ | $\rho_1=0.2$ | $\rho_1=0.3$ | $\rho_2=0.4$ | $\rho_2=0.5$ | |
|---|---|---|---|---|---|
| $a=1$ | 0.6894 | 0.7131 | 0.7382 | 0.7646 | 0.7929 |
| $a=3$ | 0.5705 | 0.6065 | 0.6440 | 0.6833 | 0.7247 |
| $a=5$ | 0.5131 | 0.5556 | 0.5996 | 0.6456 | 0.6937 |
| $a=7$ | 0.4759 | 0.5227 | 0.5712 | 0.6216 | 0.6742 |
| $a=9$ | 0.4487 | 0.4988 | 0.5506 | 0.6043 | 0.6602 |
表2: 最適な$\rho_2$を与えたときの目的関数値
| $\rho_1=0.1$ | $\rho_1=0.2$ | $\rho_1=0.3$ | $\rho_2=0.4$ | $\rho_2=0.5$ | |
|---|---|---|---|---|---|
| $a=1$ | 5.6819 | 6.5763 | 7.7925 | 9.5255 | 12.1569 |
| $a=3$ | 9.6313 | 11.185 | 13.3332 | 16.4536 | 21.298 |
| $a=5$ | 13.0465 | 15.1562 | 18.0952 | 22.4003 | 29.1491 |
| $a=7$ | 16.2407 | 18.8638 | 22.5351 | 27.9411 | 36.4666 |
| $a=9$ | 19.3051 | 22.4165 | 26.7856 | 33.2433 | 43.4706 |
これらの表から分かるように、$\rho_1$ や $a$ の値に応じて、$\rho_2$ の最適値や目的関数値が大きく変化する。特に、$\rho_1$ を増やすと目的関数値が大きく増加する。例えば、$a=9$のとき、$\rho_1$ を $0.4$ から $0.5$ へ増やすだけで、目的関数値は $10.23(+33.8\%)$ も増加している。このように、$\rho_1$ は実行速度に影響を与えるパラメータであるため、使用可能なメモリ量を加味して慎重に決めなければならない。
なお、実用上は、エントリの検索に用いるキーが一様分布に従うことはなく、テーブル内に存在するキーが検索に用いられる可能性が高い。そのため、上記の表の値より少し小さな値を用いたほうがパフォーマンスが向上する可能性がある。
数値実験#
上記の解析結果を数値的に確かめるために、数値実験を行った。
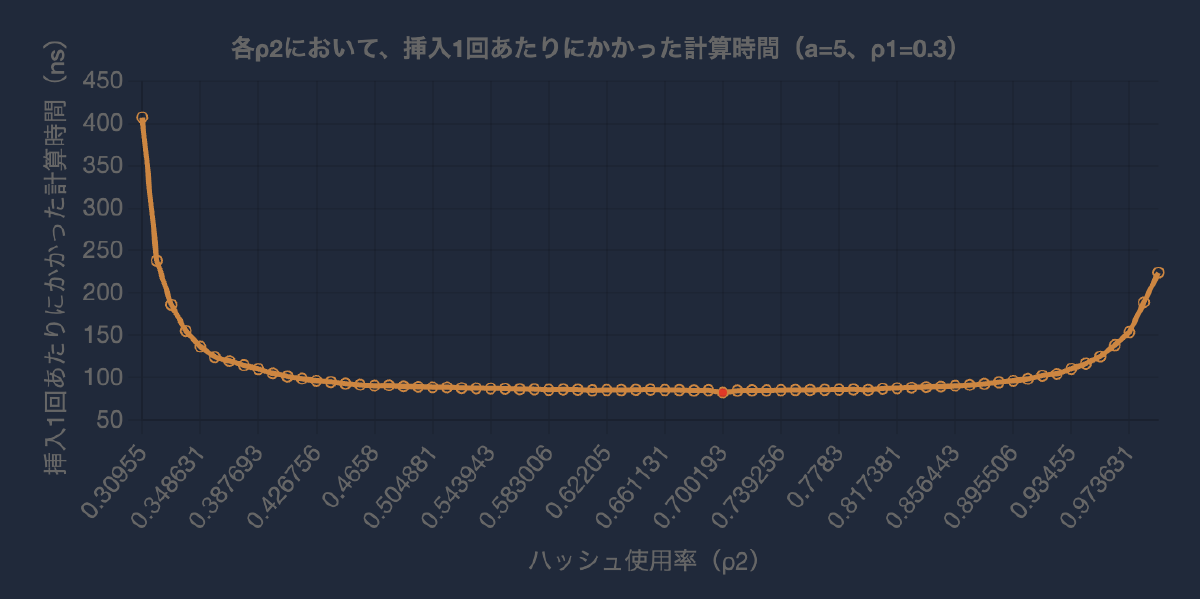
パラメータ $a=5, \rho_1=0.3$ に対し、$\rho_2$ の値を様々に変えたときの実行時間を測定した。測定結果のグラフを以下に示す。
理論的に予測した通り、挿入1回あたりの実行時間は下に凸なグラフになった。特に、 $\rho_2=0.7002$ のときに挿入1回あたりの実行時間は最小となり、その値は 82.516 nsだった。ただし、グラフから読み取れる通り、$\rho_2 \in [0.4, 0.8]$ の区間は実行時間にあまり差がなく、実用上は $\rho_2$ の値をもう少し大きく取ってGC頻度を抑えても実行時間にそれほど影響がないと考えられる。
まとめ#
本ページでは、線形走査法を用いるハッシュテーブルにおいて、 GCを行うタイミングやGCで削除するエントリ数についての考察を行った。比較回数の期待値を近似した最小化問題を解くことで、これらのパラメータの最適値を求めることができた。また、数値実験を行い、GCタイミングはあまり重要ではないことを確認した。